Rossi Tissue Equivalent Proportional Counter (ca. 1960)

The Rossi Chamber is a proportional counter that employs a spherical chamber with tissue equivalent walls and a tissue equivalent fill gas. Its purpose is to measure the dose and/or dose equivalent to small volumes of human tissue. This particular chamber was actually used by Harold Rossi at Columbia University!

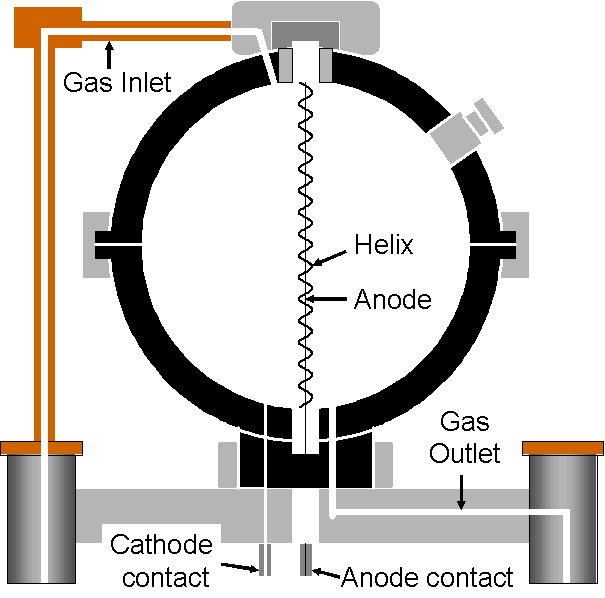
The spherical shape of the chamber was chosen so that its response would be more or less independent of the direction from which the radiation comes (i.e., it is angularly independent). However, using a wire running along the diameter of the sphere as the anode complicates this because the electric field can become distorted towards the ends of the anode where the latter gets close to the detector wall (the cathode). Because of this distorted field, gas multiplication would be decreased for the ionizing events that occur towards the ends of the anode.

To prevent this, and create a cylindrically symmetrical electric field along the length of the anode, the latter is surrounded by a fine helical wire. Unfortunately, this helix is susceptible to vibration and such vibration can result in microphonic noise (i.e., spurious counts).

The arrow in the photograph to the left is pointing towards the helical wire that surrounds the anode. The inside of the chamber is visible through a small port in the wall of the chamber that is normally sealed with a plug.

Tissue equivalent proportional counters (TEPCs) have been used for many years in microdosimetry wherein the dose or dose equivalent to small volumes of tissue (e.g., 1 um) is measured. The exact volume depends on the pressure of the fill gas.

Gamma rays or neutrons interacting with the tissue equivalent wall of the chamber "knock" charged particles across the tissue equivalent gas that fills the chamber. The size of the pulse reflects the ionization produced in the gas by the particle. As such, the pulse size also reflects the absorbed dose to the gas per particle (e.g., per neutron).

By measuring the size of each pulse, we can measure the absorbed dose (D) per particle in the gas. We could also calculate the dose equivalent (H) per particle if we could knew the quality factor (Q) since H = D Q.

One way to estimate Q would be to calculate the LET of the particle because the quality factor is derived from the LET. If we knew its path length (l) in the detector gas, we could calculate the LET of the particle using the equation LET = ,/l. (where , is the energy imparted to the detector gas per particle). While the energy transferred (imparted) to the gas per particle (,) can be measured, we don’t know the particle's path length (l). As such we can’t determine the LET.

However, if the detector chamber has a known geometry, and it does, we can calculate the average path length (lave) of the particles traversing the chamber. This allows us to calculate the lineal energy (y), a quantity closely related to the LET, using the equation: y = ,/lave. Even though the value assigned to Q is conventionally based on the LET, it is recognized that there is good reason to employ the lineal energy to calculate Q, and the ICRU has generated a curve that relates the quality factor to the lineal energy.

Since the lineal energy (y) is directly related to the energy deposited in the gas by a particle (,), it is also directly related to the pulse size. This means that pulse height analysis of the TEPC output generates a lineal energy spectrum. The higher the lineal energy, the higher the channel number a given pulse is sorted into. By using the ICRU or ICRP recommendations regarding the relationship between the lineal energy and the quality factor (Q), a value for Q can be assigned to each channel number.

We can now calculate the dose equivalent (H) per pulse because we know both the absorbed dose (D) and the quality factor (Q).

Donated by Columbia University.